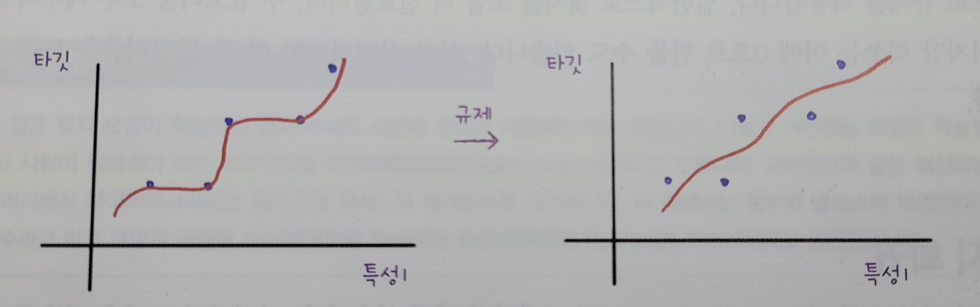
훈련세트로 훈련하면, 보통 훈련세트의 R^2값이 더 높게 나온다.
훈련세트 R^2 >> 테스트세트 R^2
- 과대적합 overfitting: 실전 투입 시, 새로운 샘플에 대한 예측값이 잘 맞지 않는다.
- 해결책
- k 개수를 올려서, 여러 데이터를 반영
- 이웃의 개수를 늘이면 데이터 전반에 있는 일반적인 패턴을 따른다.
훈련세트 R^2 << 테스트세트 R^2 또는 둘다 낮은 경우
- 과소적합 underfitting: 모델이 너무 단순해서 훈련세트에 적절히 훈련되지 않은 경우
- 해결책
- k 개수를 내려서 모델을 복잡하게 혹은 국지적인 패턴에 민감하게 변경
- 이웃의 개수를 줄이면 훈련세트에 있는 국지적인 패턴에 민감
- 모델을 조금 더 복잡하게 설계
- 훈련세트와 데이터의 세트의 크기가 작기 때문에 발생.
In [1]:
import numpy as np
perch_length = np.array([8.4, 13.7, 15.0, 16.2, 17.4, 18.0, 18.7, 19.0, 19.6, 20.0, 21.0,
21.0, 21.0, 21.3, 22.0, 22.0, 22.0, 22.0, 22.0, 22.5, 22.5, 22.7,
23.0, 23.5, 24.0, 24.0, 24.6, 25.0, 25.6, 26.5, 27.3, 27.5, 27.5,
27.5, 28.0, 28.7, 30.0, 32.8, 34.5, 35.0, 36.5, 36.0, 37.0, 37.0,
39.0, 39.0, 39.0, 40.0, 40.0, 40.0, 40.0, 42.0, 43.0, 43.0, 43.5,
44.0])
perch_weight = np.array([5.9, 32.0, 40.0, 51.5, 70.0, 100.0, 78.0, 80.0, 85.0, 85.0, 110.0,
115.0, 125.0, 130.0, 120.0, 120.0, 130.0, 135.0, 110.0, 130.0,
150.0, 145.0, 150.0, 170.0, 225.0, 145.0, 188.0, 180.0, 197.0,
218.0, 300.0, 260.0, 265.0, 250.0, 250.0, 300.0, 320.0, 514.0,
556.0, 840.0, 685.0, 700.0, 700.0, 690.0, 900.0, 650.0, 820.0,
850.0, 900.0, 1015.0, 820.0, 1100.0, 1000.0, 1100.0, 1000.0,
1000.0])
from sklearn.model_selection import train_test_split
train_input, test_input, train_target, test_target = train_test_split(perch_length, perch_weight, random_state=42)
## 아래 -1으로 지정하면 나머지 원소 개수로 모두 채우라는 의미
train_input = train_input.reshape(-1, 1)
test_input = test_input.reshape(-1, 1)
print(train_input.shape, test_input.shape)
from sklearn.neighbors import KNeighborsRegressor
knr = KNeighborsRegressor()
## k-최근접 이웃 회귀 모델 훈련
knr.fit(train_input, train_target)
print("R^2 = 1 - { sum[(타깃 - 예측)^2] / sum[(타깃 - 평균)^2 }")
print("test set R^2(결정계수):", knr.score(test_input, test_target))
print("train set R^2(결정계수):",knr.score(train_input, train_target))
(42, 1) (14, 1)
R^2 = 1 - { sum[(타깃 - 예측)^2] / sum[(타깃 - 평균)^2 }
test set R^2(결정계수): 0.992809406101064
train set R^2(결정계수): 0.9698823289099254
위의 결과는 훈련세트보다 테스트 세트의 점수가 높다 => 과소적합
- 해결책: k의 개수를 기본 5에서 3으로 조정.
In [2]:
knr.n_neighbors = 3
## 모델을 다시 훈련
knr.fit(train_input, train_target)
## 모델 평가지표 확인
print("R^2 = 1 - { sum[(타깃 - 예측)^2] / sum[(타깃 - 평균)^2 }")
print("test set R^2(결정계수):", knr.score(test_input, test_target))
print("train set R^2(결정계수):",knr.score(train_input, train_target))
R^2 = 1 - { sum[(타깃 - 예측)^2] / sum[(타깃 - 평균)^2 }
test set R^2(결정계수): 0.9746459963987609
train set R^2(결정계수): 0.9804899950518966
테스트 세트의 점수는 훈련세트보다 낮아졌음 => 과소적합 문제 해결.
두 점수 차이가 크지 않으므로 이 모델이 과대적합 된 것 같지 않다.
'책[이해 및 학습]' 카테고리의 다른 글
| 2. [혼자 공부하는 머신러닝/딥러닝] 인공 신경망(ANN) (0) | 2024.03.09 |
|---|---|
| 1. [혼자 공부하는 머신러닝/딥러닝] 로지스틱 회귀로 분석 (0) | 2024.03.09 |
| 08_선형 회귀 & polynomial regression (0) | 2023.01.03 |
| 6. [혼자 공부하는 머신러닝] 회귀(Regression): k-최근접 이웃회귀 (0) | 2023.01.03 |
| 3. [혼자 공부하는 머신러닝/딥러닝] 심층 신경망(DNN) (0) | 2022.07.22 |



